金融时间序列分析：Python基于garch模型预测上证指数波动率、计算var和var穿透率、双尾检验-你的通用数字钱包

全国数字货币钱包安装地址：tp9.app，bit16.app，tp784.app，tp888.app，im784.app，im45.app，tokenn.app，imtooken.app，imgw.app，imtom.vip，imtokemn.app，im116.app，imtokne.app，immtoken.app，im钱包.com，imtkem.app，tokim.app，im87.app，tptoka.app，tp钱包.cn，im112.app，im1.app，bitpia.app，imzg.app，imkem.vip，im70.app，im003.app，im82.app，tokim.app，imqb.app，tookeni.app，a471.cc，tokne.app，tokonii.app，imtokes.app，im1122.app，imkct.app，imkd.app，imkct.app，imtek.app，im22.im，imken.app ，tp114.app，bit114.app，imkenn.app，tp115.app，bit115.app，im221.cn，im888.app

在金融风险管理的范畴内，准确计算风险价值（VaR）至关重要，然而这一过程相当繁琐，需要运用众多模型和分布假设，这对从业者的专业能力提出了很高的要求。

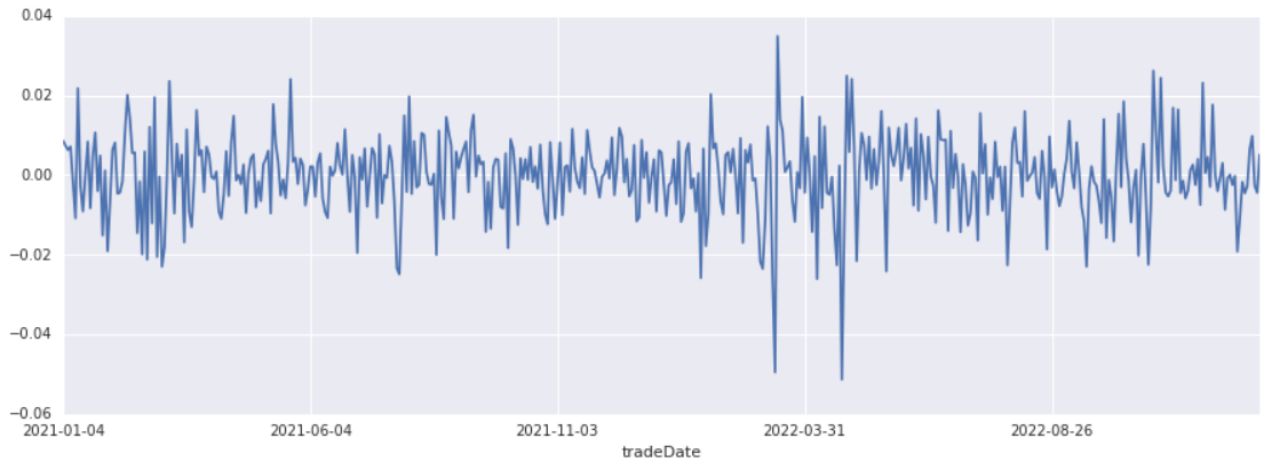
分析BNB币的市场预测模型：如何利用数据分析进行投资_货币分析模型_币种分析工具

1.正态分布下VaR计算的基础

在假定收益波动遵循正态分布的前提下，计算VaR是常见的做法。不少人在风险评估初期便采纳了这一方式，如部分传统金融机构在20世纪初便开始尝试。其核心是运用预测的波动率来不断更新VaR值。首先，计算收益率序列的均值与标准差，接着依据设定的置信水平，如常见的95%或99%，借助正态分布的累积分布函数的逆运算——Z分数，确定相应的VaR值。此法简单易懂，在市场相对平稳时具备一定准确性。但若市场遭遇极端状况，其弊端便显现，因为实际金融市场的收益率序列往往并不符合正态分布。

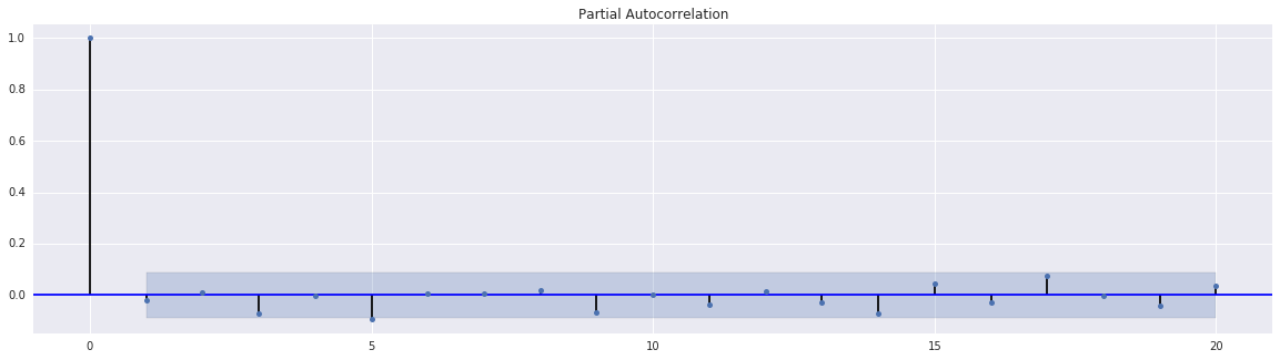
货币分析模型_币种分析工具_分析BNB币的市场预测模型：如何利用数据分析进行投资

在这种情境下，VaR穿透率较低往往意味着更强的风险管控水平。然而，仅凭这一指标无法全面反映风险管理的质量。实际上，有些金融机构过分依赖这一指标，结果在遭遇极端市场波动时，承受了严重的损失。

2.重尾分布下的VaR计算

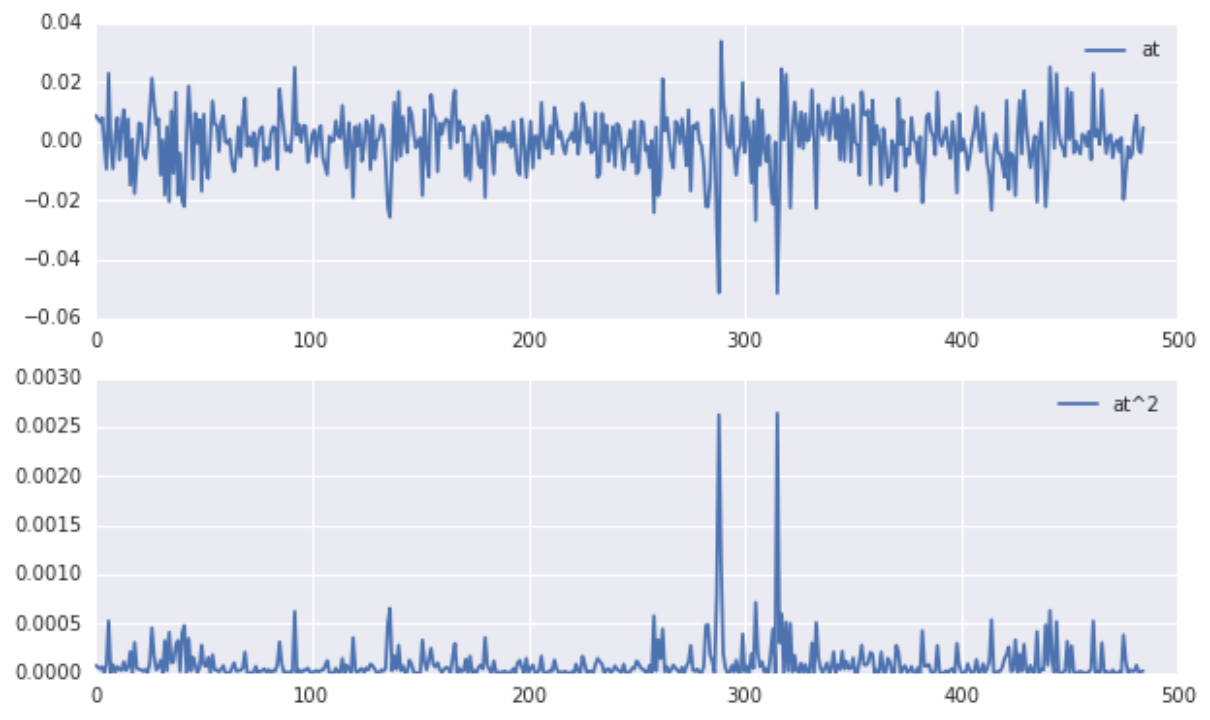
币种分析工具_分析BNB币的市场预测模型：如何利用数据分析进行投资_货币分析模型

金融数据常常呈现出厚尾特性，因此，在计算VaR时，选用适合的重尾分布进行收益率的假设更为妥当。比如t分布或Gumbel分布。t分布特别适合反映股票收益率的非正态性质，尤其在尾部表现出的厚尾现象。运用这种分布假设进行VaR计算，有其特定的方法。以股票市场为例，在新兴市场数据中，使用t分布假设得出的VaR与基于正态分布假设的结果可能存在显著不同。这种差异可能会影响投资者对风险的评估和应对措施，若投资者依据错误的VaR结果作出决策，可能会面临重大损失。

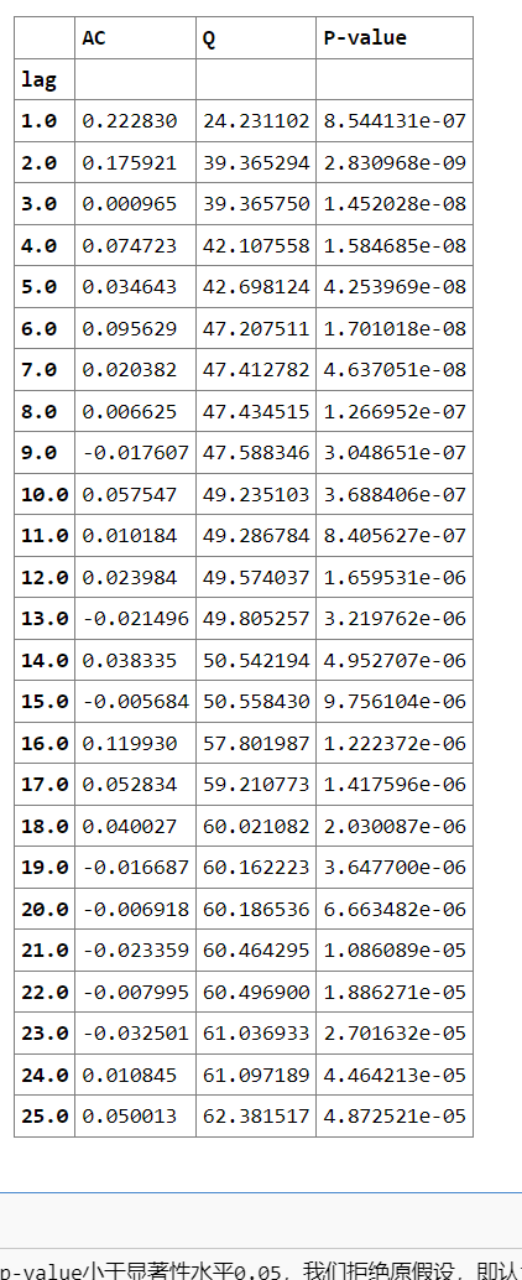
货币分析模型_币种分析工具_分析BNB币的市场预测模型：如何利用数据分析进行投资

这也说明，在实际的金融领域里，各种分布假设对风险评价起着关键作用。虽然t分布的计算过程较为繁琐，但它却能够更精确地展现市场的实际情况。

货币分析模型_币种分析工具_分析BNB币的市场预测模型：如何利用数据分析进行投资

3.序列的平稳性检验

计算结果显示p值仅为0.0，低于显著水平，因此我们否定了原假设，认定该收益率序列是平稳且非白噪声的。这一发现对金融时间序列分析至关重要。回顾2008年金融危机，众多金融模型失败的一大因素便是未能准确识别收益率序列的特性。平稳的非白噪声序列表明它具备某种规律性。在金融数据分析实践中，确认这一特性后，我们便能着手构建合理的模型并进行深入分析。这对金融从业者来说，意味着能在海量数据中筛选出有价值的信息，以支持投资决策等。若忽视这一环节，后续构建的模型可能存在偏差，无法实现预期的风险管理和投资预测目标。

4.AR均值方程的作用

币种分析工具_分析BNB币的市场预测模型：如何利用数据分析进行投资_货币分析模型

在金融序列分析中，AR均值方程发挥着重要作用。它能够描绘序列的长期走势和平均状况。以某银行股票的收益率为例，该方程能够展示出2010至2020年间的长期走势，并对序列进行预测和模拟。这对于投资者来说十分有益，他们可以依据预测结果调整投资计划。此外，该方程还能精确地区分序列中的信号与噪声。在数据交易日益繁荣的当下，这有助于排除干扰数据，更有效地把握投资机会或风险点。

分析BNB币的市场预测模型：如何利用数据分析进行投资_货币分析模型_币种分析工具

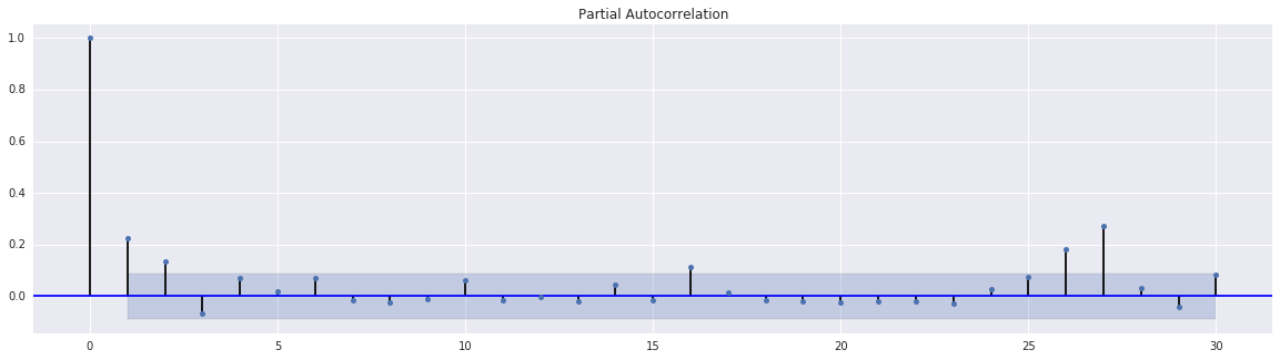
5.Ljung-Box混成检验与ARCH效应

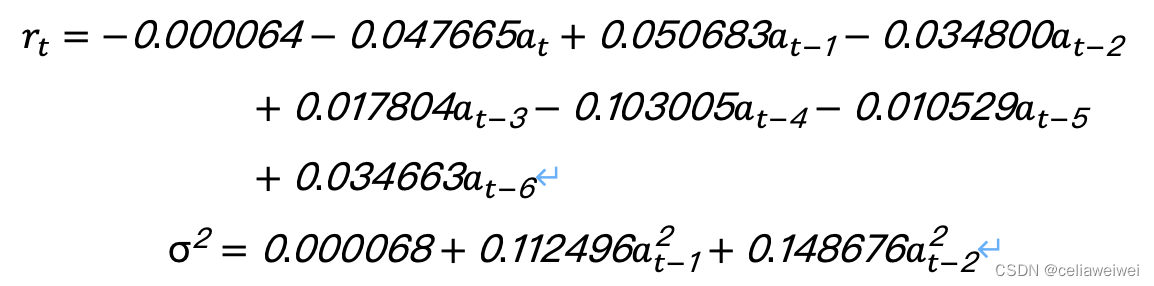
货币分析模型_币种分析工具_分析BNB币的市场预测模型：如何利用数据分析进行投资

Ljung-Box检验用于评估残差序列的相关性，是判断是否存在ARCH效应的关键方法。所谓ARCH效应，就是指序列中存在自相关的非同质性方差，即波动幅度与之前波动幅度有关。在分析某只股票的日收益率序列时，通过观察相关图形，我们注意到序列的p值普遍低于0.05的显著性水平。这表明存在ARCH效应。据此，我们建立了ARCH(3)模型。这种模型在金融分析中非常常见，它能捕捉到序列的波动和波动特征，从而提供更精确的预测和分析。这有助于金融分析师更深入地理解市场波动规律，为投资者提供更全面的风险警示。

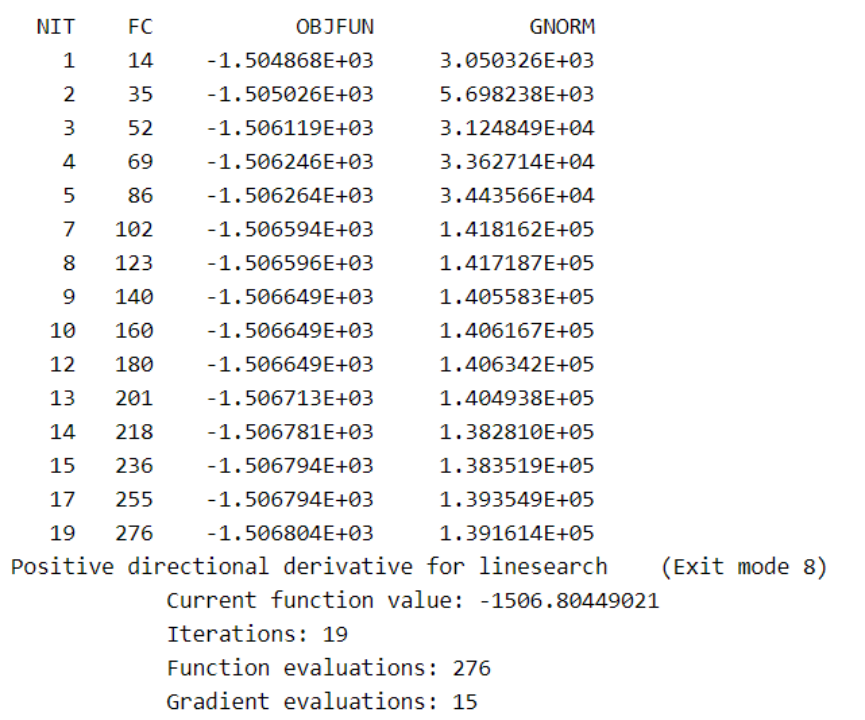
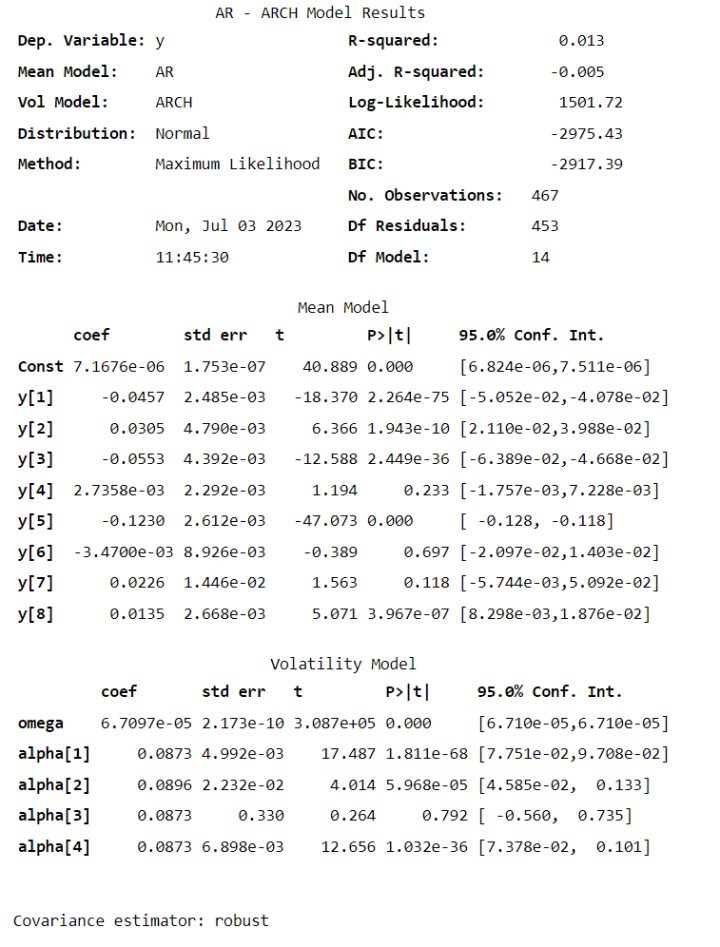
6.GARCH模型的构建与分析

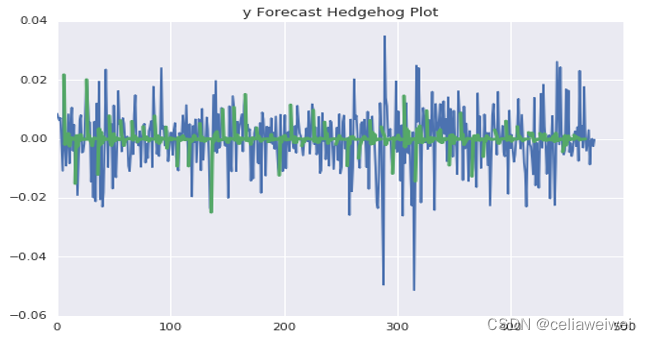
分析BNB币的市场预测模型：如何利用数据分析进行投资_币种分析工具_货币分析模型

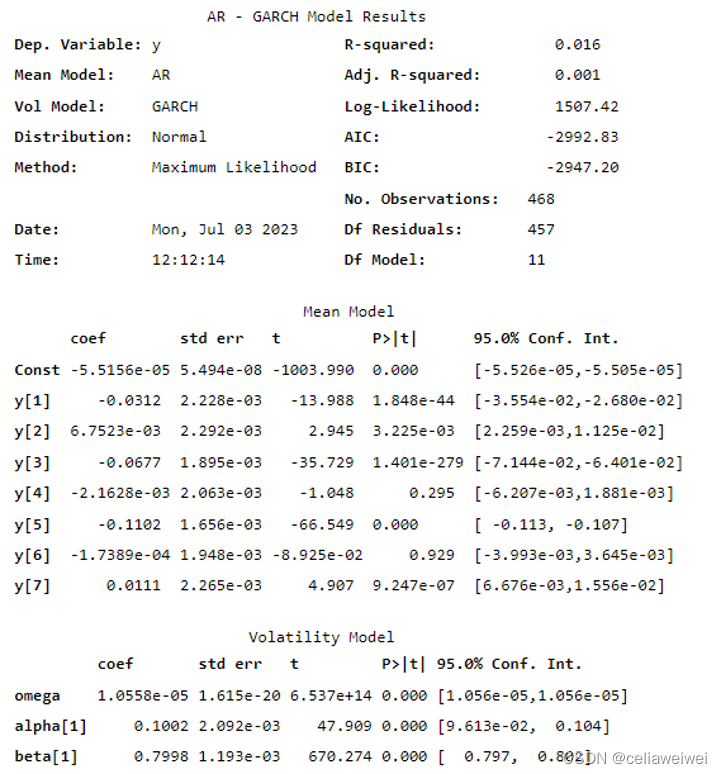
我们建立了AR(7)均值方程和GARCH(1,1)波动率模型的G(GARCH)模型。首先从回归结果着手分析，接着利用波动率模型预测波动率。我们将原始数据、拟合后的条件异方差数据和预测数据一同绘制图表，以便再次分析波动率预测的效果。这样能直观地展示预测的精确度。在现实应用中，例如在大型投资公司的风险预测部门，他们每日都会运用此模型进行风险评估。该模型有助于深入探究序列的波动特性。这对于在变幻莫测的金融市场中保障投资安全至关重要。

币种分析工具_分析BNB币的市场预测模型：如何利用数据分析进行投资_货币分析模型